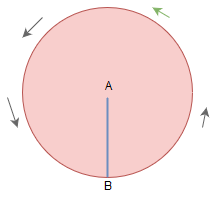
Definition of circle Circumference, Area, Chord, Segment

Definition of circle

When a line AB rotate by 360 degree taking center A, thus obtained figure is called circle.

A is called center of circle. A to any point on the circle joining is called radius, a line passing through the center of the circle is called diameter of circle and its value is 2 * radius.

The ratio between circumference to diameter is always constant and denoted by $\pi$ its value is $\frac{22}{7}$ or 3.14 approximately.

circle

$\frac{pI}/D= \pi$

Circumference of circle

so circumference of circle (p)= $\pi*D=2*\pi*r$

Area of circle formula

Area of circle= $\pi*r^2=pi*\frac{d^2}{4}$
= $4*\pi^2*r^2/4*pi={(2*\pi*r)}^2/4*pi=(oce)^2/4pi$

We divide a circle in to many small sectors, thus the length of an arc is reached near about the length of chord.

Then merge them as below we have obtained a ractangle.

Length of Chord

drawit-diagram-5
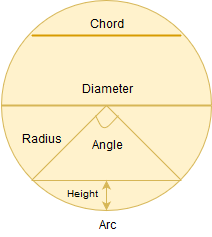
Length of chord= $\frac{a^2+h^2}{2h}$
where 2a=lengh of chord
h= height of arc
r=radius of circle
$h=r+-\sqrt(r^2-a^2)$

length of arc= arc/oce=Angle in degree/360
Radion: If are is equal in length to the radious, then the angle for form are called radion.

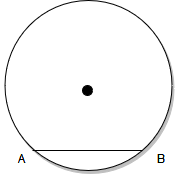
Segment of a circle

chord AB of a circle divides the circular region into two part, each part is called a segment of the circle.

segment
Sector of the circle– the area surrounded by an arc and the two radius joining the end point of the arc with the center is called a sector of the circle.
sector

Concentric circle– two or more circles with the given centre are called concentric circle.