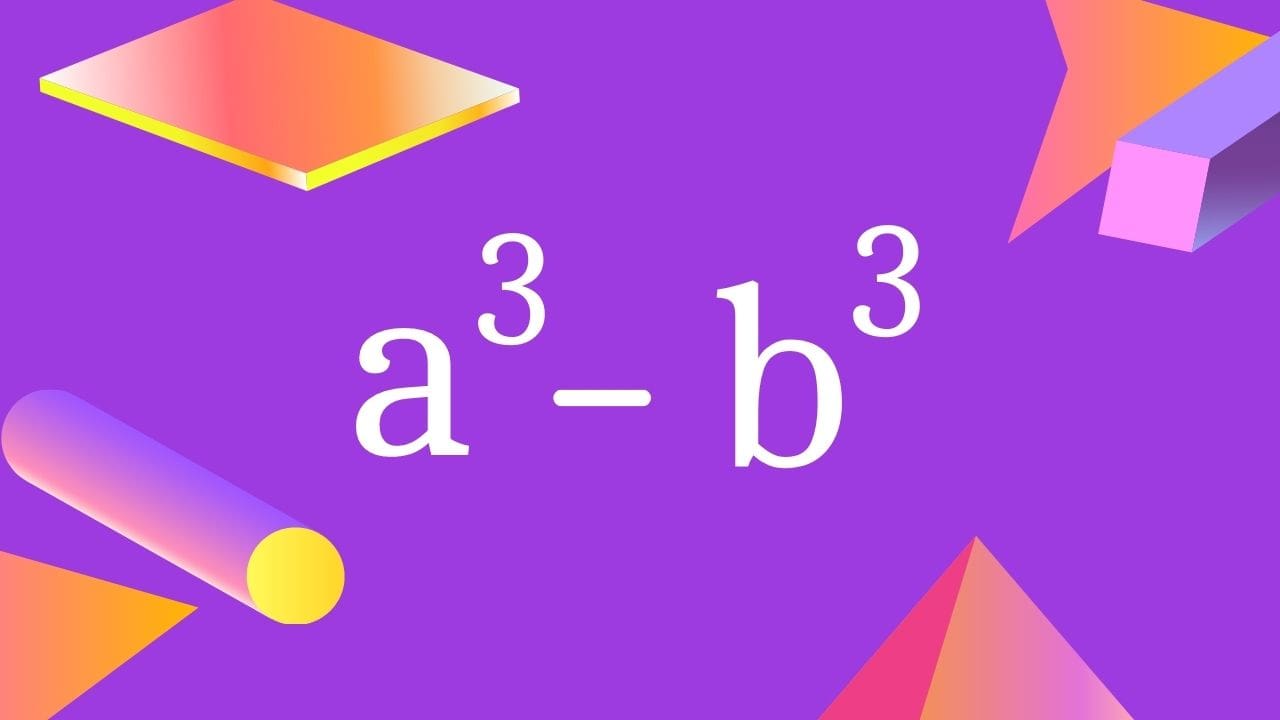What Is a cube minus b cube a³ – b³?
The a³ – b³ formula is known as the subtraction of cubes (of two numbers) formula.
It is simply read as a cube minus b cube. Without actually calculating the cubes, the cube minus b cube formula is used to find the difference between the two cubes.
It is also used to factorize the binomials of cubes, solve mathematical equations, and more.
The a³ – b³ formula is also known as one of the most important algebraic identities.
So it is worth memorizing so that one does not stick in the answer whenever it is required.
What Is a³-b³ Equals To?
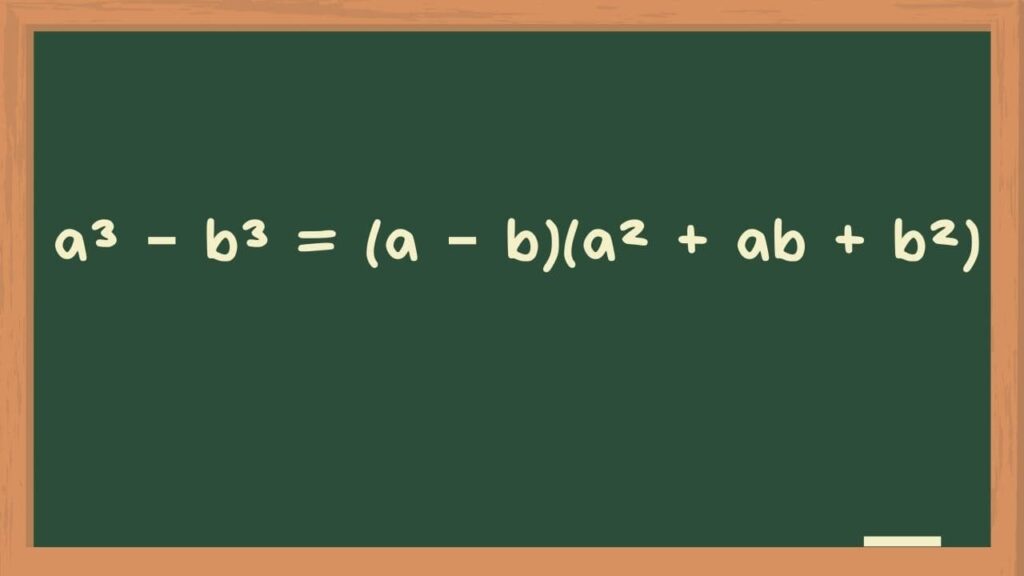
Expressed in words, the subtraction of the cubes of two numbers is the product of the difference between the two numbers by the “imperfect square of the sum.”
The cube minus b cube formula or the difference of cubes formula is :
a³ – b³ = (a² + ab + b²) (a – b)
What Is Algebraic Formula?
Algebra includes both letters and numbers. Letters or alphabets are used to show the unknown quantities in the algebra formula.
Numbers are fixed, i.e. their value is known. Now, a combination of letters, numbers, factorials, matrices, etc. is used to form a formula or an equation.
This is basically the methodology for algebra.
Therefore, we can say that algebraic formula is a rule or an equation written using algebraic and mathematical expression consisting of numbers, variables (unknown values), and mathematical functions (addition, subtraction, division, multiplication, etc.).
They are basically used to find elements of polynomials. It is an equation that involves algebraic expressions on both sides that are set equal to each other.
The algebraic formula is a short and quick formula to solve complex algebraic calculations.
There are certain very important algebraic equations and formulas that students must learn for their exams.
These formulas are the foundation of elementary or basic algebra.
Here, we will provide a list of some important algebra formulas or identities.
The comprehensive list will help the students to refer to it whenever they wish or have a quick revision before exams.
Tips: Only rote learning is not enough. You must also understand the concept behind the identity and learn how to effectively apply these identities to a problem correctly.
Standard Algebraic Identities
Four standard algebraic identities are listed below:
Identity-1: Square of Sum of Two Terms
(a + b) (a + b) or (a + b)²=b² + 2ab + a²
Identity-2: Square of Difference of Two Terms
(a – b) (a – b) or (a – b)² =b²–2ab + a²
Identity-3: Difference of Two Squares
(a – b) (a + b)=a² – b²
Identity-4:
(x + b) (x + a) = ab + (a + b)x +x²
Algebraic Identities Derived by Binomial Theorem
Identity- I: (a + b)² = a² + 2ab + b²
Identity-II: (a–b)² = a² –2ab + b²
Identity-III: (a+b) (a–b)=a²– b²
Identity- IV:(a–b)³= a³ –b³ – 3ab (a – b)
Identity-V:(a + b + c) (a² + b² + c² – ab – bc – ca) = a³ + b³ + c³ – 3abc
Identity- VI: (x + a) (x + b) = x² + (a + b)x + ab
Identity- VII:(a + b + c)² = a² + b²+ c² + 2ab+2bc+ 2ac
Identity- VIII: (a + b)³=a³ + b³ + 3ab (a + b)
Factorizing Algebraic Identities
- a² – b² (Read as a square minus b square) = (a + b) (a – b)
- a³ – b³ (Read as a cube minus b cube) = (a – b) (a² + ab + b²)
- a³ + b³ (Read as a cube plus b cube) = (a + b) (a² – ab +b²)
- a⁴ – b⁴ (Read as a raised to the power 4 minus b raised to the power 4) = (a² – b²) (a² + b²)
Trinomial Algebraic Identities
- (b + c) (a + c) (a + b) = (ac + bc + ab) (a + b + c) – abc
- c³+b³ + a³ – 3abc =(a² + b² + c² – ab– bc – ca) (a + b + c)
- c² + b² + a² = (a + b + c)² – 2 ( ac + bc + ba)
- (a – b) (a – c) = bc – (b + c) a + a²
What Is The Easiest Way To Remember Algebraic Formulas?
Tips to memorize algebraic formula:-
- Use number of channels to learn the formula.
- Familiarize yourself in advance with the formula. It’s a great idea to read the upcoming topics in your textbook before going to school.
- Avoid Distractions.
- Practice problems daily will help you to remember the formulas.
Difference Between An Algebraic Expression And Identities
Many times students get confused between expressions and identities. Hereinafter laid down are some differences between them.
- An algebraic expression can be defined as a mathematical statement that consists of variables/numbers including an arithmetic operation between them while algebraic identities is an equivalency link such as X=Y. This implies that X and Y include some variables. Also, X and Y deliver the same value as each other in spite of the values that are covered for the variable.
- An algebraic expression in general is an expression that comprised constants and variables and a variable can accept any value. Therefore, the expression value can alter if the variable values are altered/changed/switched.On the contrary, algebraic identity is true for all the values of the variables.
- For example, 6q + 3 isan algebraic expression where 6q and 3 are the terms and “q” denotes the variable of the provided expression. Here the variables and terms are separated by an arithmetic sign/symbol +. Let us understand the difference between an algebraic expression and identities with the help of another example–8x + 5 = 20 where 8x + 5 is the left-hand side (LHS) of the identity and 20 is the right-hand side (RHS) of the identity. The equal sign within the LHS and RHS symbolizes that the value of LHS is identical to the RHS of the identity.
Proof Of a³-b³ Formula
Let’s prove whether this a³-b³ = (a- b) (a²+ab+b²) formula is right or wrong ?
For this we need to prove Left hand side (LHS) = Right hand side (RHS). Let’s start our proof with the steps mentioned below :-
LHS (Left Hand Side) = a³ – b³ (Read as a cube minus b cube)
On Solving RHS side we get,
= (b² + ba + a²) (a – b)
On multiplying the a and b separately with (a²+ ab + b²) we get,
= a (b² + ba+ a²) – b(b² + ba + a²)
= b²a + a²b – b³ + a³ – ba² – ab²
= a²b – a²b + ab²- ab² + a³ -b³ [by bringing the like terms together and cancelling the possible terms such as ba² and b²a in the right hand side term]
= a³ – 0 – b³
= a³ – b³
Hence proved, LHS = RHS
Let us prove also this by putting
a = 5 and b= 3 then,
LHS = a³ – b³
LHS = 5³-3³
LHS = 125 – 27
LHS = 98
RHS = (a – b)(a² + b²+ ab)
RHS = (5-3)(5²+3²+ 5×3)
RHS = (2)(25+9+15)
RHS = 98
∴ LHS = RHS, Hence proved.
How To Derive a Cube Minus b Cube Formula?
As we know that,
(a−b)³ =a³ – b³ – 3a²b + 3ab²
⇒a³ – b³ =(a – b)³ + 3a²b – 3ab²
⇒a³ – b³ = 3ba (a – b) +(a – b)³
Now taking (a – b) common we have,
⇒a³-b³ =(a−b)[(a−b)²+3ab]
Since, we know that
(a−b)² = a²+b²−2ab
Using this property in the equation mentioned above, we get –
⇒ a³ – b³ = (3ab – 2ab + b² + a²) (a – b)
Simplifying the aforementioned equation that we have, we get –
⇒ a³ – b³ = (ba + b² + a²) (a – b)
Hence, it is the required formula of a³-b³.
Note-The formula for (a−b)³ can easily be derived by writing (a−b)³ = (a−b)(a−b)². Then using the identity i.e.(a−b)² = a²+b²−2ab
So, (a−b)³ = (a−b)(a²+b²−2ab)
On simplification of this right hand side will help us getting the value of(a−b)³.Whenever we find difficulty in remembering this formula then the above steps helps to derive it immediately.
Some examples using a³ – b³= (b² + ba + a²) (a – b) formula
Solving some good questions can aid you in understanding thisa³ – b³= (b² + ba + a²) (a – b) formula in detail.
Example 1: Find the value of 100³- 8³ by using this formula.
Solution: In this question, we have to find: 100³- 8³. Here we will assume that a = 100 and b = 8. So we will replace these a and b with 100 and 8 respectively in the formula of a³ – b³= (b² + ba + a²) (a – b)
100³-8³ = (100-8)(100²+100*8+8²)
= (92) (10000 + 800 +64)
= (92)(10864)
=999488
Answer:999488
Example 2: Factorize the following expression 8p³- 27 by using the a³-b³= (b² + ba + a²) (a – b) formula.
Solution: Here we have to factorize: 8p³- 27. We will use this formula to factorize this expression. Let us assume a = 2p and b = 3. So we can rewrite the given expression in the form of a³-b³.
8p³- 27 = (2p)³- 3³
Since, a³-b³= (b² + ba + a²) (a – b)
(2p)³-3³ =(2p-3)((2p)²+(2p)(3)+3²)
= (2p-3) (4p²+6p+9)
Answer: (2p-3) (4p²+6p+9)
Example3:If a-b=5,ab=20, find a³-b³ ?
Solution: Since (a – b) = 5
Cubing both Sides, we get,
(a-b)³ = 5³
a³-b³-3ab(a-b) = 125
Substituting the value of (a – b) and ab, we get
a³-b³-3*20(5) = 125
a³-b³-300 = 125
a³-b³ = 125 + 300
= 425
Answer: a³-b³ = 425
Example 4: Factorize the expression 27x³– 125 using a³-b³ formula.
Solution: To factorize: 27x³ – 125.
We can write the given expression as,
27x³ – 125 = (3x)³– 5³
We will substitute a = 3x and b = 5 in the formula of a³– b³.
a³– b³ = (b² + ba + a²) (a – b)
(3x)³-5³ =(3x-5)((3x)²+(3x)(5)+5²)
= (3x-5) (9x²+15x+25)
Answer: (3x-5) (9x²+15x+25)
Common Examples & Applications Of a³-b³Use In Daily life
- Making a schedule of activities
- Catching the ball game played by 5-6 year-old kids
- A kid developing spatial intelligence
- Computer Programming
- Astrological calculations
- Shopping
- Finding the tax liability
- Preparing the food or halving/doubling the recipe
- Technological developments
- Budgeting
- Doing Interiors and Landscape designing
- Professional Sports
- Real Estate Project Planning
Frequently Asked Questions:
- How To Use the a³– b³ Formula?
The following steps are followed while using a³– b³formula. Firstly, one should note the pattern of the Nos whether they have ^3 as power or not. Write down the formula of a³– b³.
a³ – b³ = (b² + ba + a²) (a – b)
Putting the values of a and b in the a³ – b³ formula and simplify it.
- Is a^2the same as 2a?
No, a^2 is not same as 2a. “a^2” means “a” in product with itself twice. It’s a very simple notation. And “2a” means that you have a variable “a” summed with itself 2 times. In the first case, it is the multiplication of said number with itself and in the other case, it is the addition of a number with itself.
- How To Simplify Numbers Using the a³ – b³ Formula?
Let us understand the use of the a3 – b3 formula with the help of the following example: Find the value of 10³ – 3³ using the a³ – b³formula. Let us assume that a = 10 and b =3. We will substitute these in the formula of a³– b³.
a³ – b³= (b² + ba + a²) (a – b)
10³-3³ = (10-3)(10²+ (10)(3)+3²)
= (7) (100+30+9)
= (7)(139)
= 973
- What are the basic rules of algebra?
Distributive, associative, and commutative laws are the basic laws of Algebra. They help in determining unknown quantities, explaining the relationship between number operations, and lend towards simplifying equations or solving them.
- Is there any difference between (a³-b³) and( a-b)³. If I am writing both as same. Is there any mistake ? What’s the mistake there?
Yes, there is a huge difference between (a³-b³) and (a-b)³.
(a – b)³ [Read as a minus b whole cube] = a³ – 3ba(a – b) – b³
Then, a³ – b³ = 3ba (a – b) + (a – b)³
= (a – b)[(a – b)² + 3ab]
= (a-b)(a² – 2ab + b² + 3ab)
= (b² + ba + a²) (a – b)