Point– a point determines a location, its has neither length nor thickness.
Line– a line is a collection of points which can be extended indefinitely on both the sides it has neither breadth nor thickness that has only length(A line consists of infinite point)
Properties – only one line can be drawn through two points a line has infinitely many points on it. Infinite lines can be drawn through a given point.
Plane: Every solid has a surface which is flat or curved. It may be smooth or rough. In geometry we take totally flat or curved surface a plane is a flat surface it has length and width but no height.
Properties of points & lines in a plane.
1. Any two points on the same plane, can be connected with one & only one line passing through them.
2. Two planes intersect in a line.
3. Intersecting lines- two line that meet at a point are called intersecting line.
Parallel line: the lines which never meet even when they are extended are known as parallel lines.
Transversals– a line intersecting two or more given lines in a plane at different point is called a transversal line.

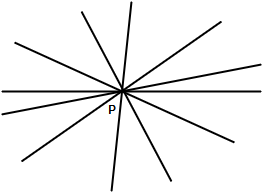
Concurrent lines– three or more lines in a plane are said to be concurrent if all of them pass through same point & this point is called the point of concurence.
Collinear points– Three or more point in a plane are said to be collinear it they all lie on the same line.
![]()
Property of divisibility
1. If a number is divisible by another number, it must be divisible by each of the factor or that number.
2. If a number is divisible by each of the two or more than two co prime numbers it must be divisible by their product.
3. If two given number are divisible by a number, then their sum is also divisible by that number.
4. If two given numbers are divisible by a number, than their difference is also divisible by that number.

