7/8 As A Percentage is 87.5 %
Percent and fractions are the two terms that we generally use in comparing quantities.
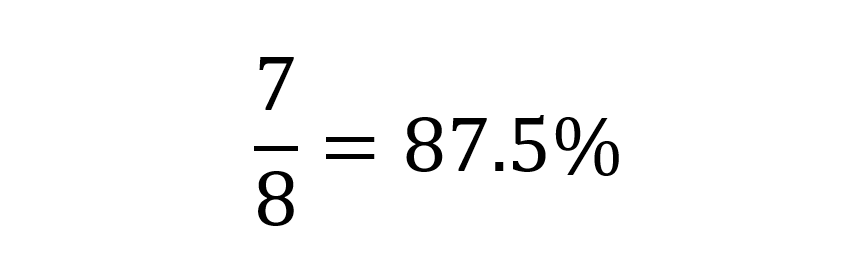
A fraction is represented as a numerical value that is defined as a part of a whole while percent, a relative value tells you how much of the whole you have and it is definitely easier to remember as compared to a fraction.
To understand the concept of percent and fraction, consider that if a party has 23 people and 15 such members are males.
Now, if it is asked what is the percentage of male students among them, then what will be your answer?
It is 15 out of 23. To simplify: 15/23 = 0.652173913 or about 65%.
If you want to know how to convert fractions to percent, you are only required to know the formula for a fraction to percent conversion.
But first of all, you need to understand what exactly is a fraction and percent in detail.
What Is A Fraction?
A Fraction refers to no of equal part/parts of a whole quantity.
It can also be represented as the number of parts of a certain size divided by the whole thing.
Brush Up Your Lessons – A fraction comprised of a denominator and a numerator.
The denominator is written below while the numerator is written above the line. The denominator represents how many parts consist of a whole, which cannot be zero while the numerator indicates some equal parts of a whole.
For example, in the fraction 7/8, Here the numerator is 7 – that means seven equal parts, and the denominator is eight – indicating eight parts make up a whole.
What Is Percent?
Percent refers to a number or ratio that is expressed as a fraction of 100. Percentage means ‘per 100’. So, when you say 100% of something, it means the whole of something.
More About Percentages – A percentage is a dimensionless number as it has no unit of measurement. It is denoted by using the percentage sign %.
Example –
- 45% can be written in a fraction as 45/100.
- In a meeting, 30% of the people were female, which means out of every 100 people, 30 were female.
Percentage Formula
A percentage refers to a ratio or number whose denominator is equal to 100.
The formula used to calculate the percentage is:=(part/whole)×100%.
For example, if we want to find 10% of 130, it can be done as10*130 /100
= 13%
Thus, 10% of 130 is 13.
Two Ways To Calculate Percentage
Ways to find a percentage are:
- The denominator of the fraction can be changed to 100.
- By using the unitary method
Note – It should be noted that the first method for calculating percentage is not used in situations where the denominator is not a factor of 100. We use the unitary method in such cases.
Example –
Fatima’sbrothers, Akshay and Karan calculated the percentages but in different ways.
Akshay used the unitary method. Using the unitary method for calculating percentage, he was told that out of 50 bangles, the number of pink bangles are 14.
Hence, out of 100, the number of pink bangles will be 14/50 × 100= 28%.
On the other hand, Karan converted the fraction 14/50 into an equivalent fraction 28/100 by multiplying the numerator and denominator with 2/2.
So, 14/50= (14×2)/(50×2)
= 28/100
= 28%
How to Calculate Percentage Change
The percentage difference/ change is the variation in the value of a quantity or number over a while in terms of percentage.
Let us now go and learn how to calculate the percentage change between the two given numbers.
The formula gives Percentage difference or Percentage change is:
The change in percentage= 100 × [(The change in value) / Original Value]
Since Change in Value = New value – Original value
Note:
The change in the value could be negative or positive. A negative difference means that there is a percentage decrease in the value, else wise, it is a percentage increase.
The percentage is also used to compare quantities.
Let us say you are required to find the increase or decrease in the value of a certain quantity over a while; in place of quoting the numbers, this comparison can be conveniently expressed as a percentage decrease or a percentage increase in quantity.
Thus, there are 2 kinds of percentage change in maths. Let’s learn about them now!
Types Of Percentage Changes
Percentage Decrease
Percentage decrease is the difference between the initial and the final value. It shows a loss of value from the original expressed it in the form of a percentage regardless of units.
To calculate the decrease in percentage:
- Find the initial value and final value.
- Subtracting initial value from the final value.
- Divide the output by the initial value.
- Multiplying the result by 100 and finding the percentage change.
(Note: if the percent is negative, it implies the percentage change is positive.)
So, Percent Decrease = – [(final Value – initial Value) / initial Value] × 100]
Percentage Increase
A percent increase shows how much a percentage has surged over a period. In other words, a percentage increase is a difference between the original value and the increased value, expressed in the form of a percentage.
Tip – We can also use this difference to find the relative increase against the original value (or) we can say that percentage increase is a measure of percent change which gives the extent to which a quantity gains intensity, magnitude, or value. The percentage increase is calculated by :
Percentage Increase = [(Final Value – Initial Value)/Initial Value] × 100.
It is very common for individuals when they are learning about fractions, to want and know about how can they convert a fraction such as 7/8 into its percentage equivalent. We will show you how to convert any fraction into its percentage form really easily in this step-by-step guide. Here we go!
Conversion Of 7/8 As A Percentage
Let’s go over some very quick fraction basics before we get started in the fraction to percentage conversion.
Remember that a denominator is a number below the fraction line, and the numerator is the number above the fraction line. We are going to use this later in this tutorial.
Method Number 1 –
Step Number 1 – Divide the numerator part of the fraction i.e. 7 by the denominator part of the fraction i.e. 8 to retrieve the desired decimal value.
= 7/8
= 7 ÷ 8
= 0.875
Step Number 2 – In the 2nd and also the final step of this tedious calculation, you are required to multiply the above-calculated decimal value to its percentage form by multiplying with 100.
Stating numerically,
= 100 × 0. 875
= 87.5 %
Super Fun Fact –Did you know that you can also reverse step number 1 and step number and still come to the same result? Don’t believe me? Do this – If you multiply 100 by 7 as –
= 100 × 7
= 700
and then divide the result by 8,
= 700 ÷ 8
= 87.5 %
you will still come to 87.5!
Method Number 2 –
When we are dealing with percentages, what we really want to say is that the percent is also a fraction of 100.
The term “Percent” means per hundred, and so 50% is the same as saying 5/10 or 50/100 in the fractional form.
We can adjust the fraction to make the denominator part 100 as our denominator in the fraction 7/8 is 8. We divide 100 by the denominator for doing that –
= 100/8
= 100 ÷ 8
= 12.5
Once you have acquired the multiple 12.5 as above, now you can easily multiply both the numerator and the denominator by 12.5 as below –
= (7 × 12.5) / (8 × 12.5)
= 87.5 / 100
Now, as you can see that our fractional value came out to be 87.5/100. It essentially means that 7/8 in its percent format is 87.5%.
We can also work this out in a easier way by converting the fraction 7/8 into a decimal. To do that, we can simply divide the numerator by the denominator:=0.875
Now, you can multiply the aforementioned answer by 100 to convert it to its percent form since you have the answer for the above-mentioned division –
100 × 0.875 = 87.5%
And there you have 2 different solutions for the conversion of 7/8 to its percent equivalent. Both are very easy to do and straightforward methods, but I personally prefer the conversion to the decimal method as it takes few steps as compared to the other methods.
When is the conversion of fractions to their decimal values helpful and useful?
Fractional values are commonly used in our day-to-day life. You will often describe the problem using fractions if you are trying to score a test or splitting a bill.
Sometimes, you might also wish to express the given fractional value in its percentage form.
Conversion Table Of Fraction To Percentage
The fraction to percentage table is mentioned below for a few common fractions. This table will help you in solving many numerical problems in mathematics.
| Fraction | Percent |
| 1/2 | 50 % |
| 1/3 | 33.33 % |
| 2/3 | 66.67 % |
| 1/4 | 25 % |
| 2/4 | 50 % |
| 3/4 | 75 % |
| 1/5 | 20 % |
| 2/5 | 40 % |
| 3/5 | 60 % |
| 4/5 | 80 % |
| 1/6 | 16.67 % |
| 2/6 | 33.33 % |
| 3/6 | 50 % |
| 4/6 | 66.67 % |
| 5/6 | 83.33 % |
| 1/7 | 14.285714 % |
| 2/7 | 28.571429 % |
| 3/7 | 42.857143 % |
| 4/7 | 57.142858 % |
| 5/7 | 71.428571 % |
| 6/7 | 85.714286 % |
| 1/8 | 12.5 % |
| 2/8 | 25 % |
| 3/8 | 37.5 % |
| 4/8 | 50 % |
| 5/8 | 62.5 % |
| 6/8 | 75 % |
| 7/8 | 87.5 % |
| 1/9 | 11.111111 % |
| 2/9 | 22.222222 % |
| 3/9 | 33.333333 % |
| 4/9 | 44.444444 % |
| 5/9 | 55.555556 % |
| 6/9 | 66.666667 % |
| 7/9 | 77.777778 % |
| 8/9 | 88.888889 % |
| 1/10 | 10 % |
| 2/10 | 20 % |
| 3/10 | 30 % |
| 4/10 | 40 % |
| 5/10 | 50 % |
| 6/10 | 60 % |
| 7/10 | 70 % |
| 8/10 | 80 % |
| 9/10 | 90 % |
Difference Between Percentage and Percentile
Most people get confused while dealing with percentages and percentiles. To clear the air between the two, differences between both have been stated below –
- The percentage represents the number out of 100 while the percentile is not a number out of 100.
- The percentage can be written as ratios or proportions while percentile cannot be written as ratios or proportions.
- The percentage is written in the form of x% while another one is written in the form of Xth.
- The percentage is not based on ranking numbers but the percentile is based on ranking numbers.
- The percentage does not rely on the normal distribution while the percentile relies on the normal distribution.
- A percentage is obtained by multiplying the ratio of two numbers by 100 but a percentile is a percentage of values that can be found below a specific value.
Conclusion
In my life, I have seen many students get confused whenever a numerical problem comes up about how to convert a fraction to its percent form, but it should be simple if you follow the steps laid out here. That being said, you might still require a calculator for more complicated fractions.
Do This – Grab yourself a calculator, a pad, and a pen if you wish to practice, and hence try converting a few fractional values to their percentage forms by yourself.
We hope that this tutorial has helped you to understand how can you easily convert a fraction to its percentage form. You can now go forward in your life and convert as many as fractions to their percentage equivalents as your heart desires!
Frequently Asked Questions
- What is the lowest form of the fractional value 7/8?
The fraction 7/8 is itself in the lowest form as there is no whole number by which we can divide the denominator and numerator. 7 is a prime number so the fraction is in what people call its simplest form.
- How do you express7/8 as a division problem?
As you can express the fraction 7/8 as a decimal by division, you need to simply divide 8 into 7 and you get the result as 0.875.
- Is 7/8 a rational or irrational number?
Mathematically, a rational number is the ratio of an integer to a non-zero integer b. The general rule is a/b. So, 7/8 is a rational number. Hence, it is also called a fraction.
