1) Factors & Multiples– if a number A divides another number B, exactly we say that A is a factor of B. In this case B is called a multiple of A.
2) Highest common factor or a greatest common measure (CGM) or greatest common divisor. The H.C.F of two or more than two numbers is the greatest number that divides each of them exactly.
Method- factorization- express each of the given number as the product of prime factors the product of least power of common prime factors gives H.C.F.
12 = 2×2×3
18 = 2×3×3 H.C.F 2×3 = 6
Division method- to find the H.C.F of two given number divide the larger number by smaller one. now divide the divisor by the reminder, repeat the process of dividing, the proceeding number by the reminder last obtained till zero is obtained as reminder. The last divisor is the required H.C.F same procedure for more than 2 number.
e.g- H.C.F of 513, 1134& 1215
1134 ) 1215 ( 1 H.C.F of 1134 & 1215 = 81
__1134_____
81 ) 1134 ( 14
____1134____
××
H.C.F of 513 & 31
H.C.F of 513 & 81 = 27
Least common multiple (LCM) – the least number which is exactly divisible by each one of the given number is called their L.C.M.
Method- factorization- resource each one of the given numbers into a product of prime factor then L.C.M is the product of highest power so fall the factors.
e.g. 72, 108 & 2100
![]()
Common division method (shortcut method)
Arrange the given number in a row in any order, divide by a number which divides exactly at least two of the given number and carry forwarded the numbers which are not divisible. Repeat the above process till no two of the numbers are divisible. By the same number except the product of the divisor & the co divided numbers is the repaired L.C.M.
e.g- L.C.M of 16, 24, 36, 54
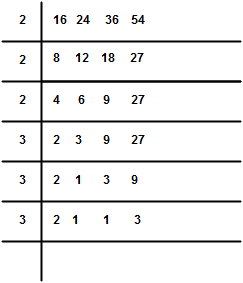
![]()
4) Product of two numbers = product of their H.C.F & L.C.M
Example ![]()
5) co- primes– the two numbers are said to be co-prime. If their H.C.F is 1
6) H.C.F & L.C.M of fractions –
![]()
Example ![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
L.C.M of 3, 9,27 81=81
![]()
![]()
H.C.F & L.C.M of decimal fraction– the given no make the same number of decimal places by annexing zero in some numbers if necessary considering these numbers without decimal point. Find H.C.F & L.C.M as the case maybe.
e.g. L.C.M & H.C.F of 0.63, 1.05 & 2.10
Without decimal- 63, 105, 210
HCF of 63, 105, 210 is 21
HCF of 0.63,0.105, 2.10 is 0.21
L.C.M of 63, 105, 210 is 630
L.C.M of 0.63, 1.05, 2.10 is 6.30
8) Comparison of Fraction– Find the L.C.M of denominator & convert them equivalent fraction with L.C.M as the denominator by multiples both the numerator & denominator.
Example ![]()
then ![]()
Typical Question:- Find the largest number which divided 62, 132, 237 to leave the same remainder in each case.
Reqd. number = H.C.F of (132-62), (237-132), & (237-62)
= H.C.F of 70,105 & 175 = 35
