A number can be represented in two ways i.e. fractions and decimals.
Fraction
A fraction or a fractional number is expressed as a numerical value that is defined as a portion or a part of a whole.
In other words, a fractional number represents the equal parts of the whole. A fraction has two parts i.e denominator and numerator.
The number on the bottom of the line is known as the denominator and the number on the top of the line is known as the numerator.
The denominator defines the total number of equal parts in a whole whereas the numerator defines the number of equal parts taken.
For example, We have a large fruit and we cut the fruit into 8 equal pieces. Then each portion of the fruit is only 1/8th of the total quantity of fruit.
Thus, 1/8 is a fraction. We do not every time deal with whole objects in our daily life.
Sometimes, we have to deal with portions or parts of whole objects. To quantify them, we need fractions. A fraction helps to make the calculation faster and judge the numbers easily.
What are the types of fractions?
Proper fractions, Improper fractions, and Mixed fractions are three types of fractions.
Proper Fractions
The numerator is smaller as compared to the denominator in this type of fraction. Example: ⅓, ⅔, ⅖, 3/4, 2/9, etc.
The quotient, or division, of a proper fraction, will always give a value lesser than 1
Improper Fractions
Improper fractions are the kind of fractions where the numerator is larger than the denominator.Example:3/2, 5/2, 7/3, 9/5, etc.
Since the value of the numerator is larger, the quotient of an improper fraction will always give a value equal to 1 or greater than 1.
Mixed Fractions
A mixed fraction is a type of fraction in which you combine a natural number and a fraction. Example : 3(½), 6(⅔)
Conversion of a mixed fraction into an improper fraction is done by multiplying the whole number to the denominator and then adding the numerator to obtain the numerator of the resulting number.
The denominator of the improper fraction will be the same as the denominator of the mixed fraction.
As mixed fractions have a whole number part, their value will be always greater than 1.
Other Types Of Fractions :
Like Fractions
Like fractions are those fractions that have the same denominators. For example: the fractions 2/9, 3/9, 5/9, and 6/9 all have the same denominator 9.
NOTE:
Simplification of like fractions is easy. For example, if you want to add the above four fractions, only you have to do is add the numerators. The denominator will remain the same.
So, (2/9) + (3/9) + (5/9) + (6/9) = (2 + 3 + 5 + 6)/9 = 16/9.
Unlike Fractions
Unlike fractions are that type of fractions that have different denominators. For example: the fractions 2/3 and ¼ have different denominators.
Equivalent Fractions
Fractions that upon simplification gives the same value are equivalent fractions. For example, ½ and 50/100 are equal to 0.5.
Unit Fractions
Unit fractions are the type of fractions whose numerator is 1 and the denominator is a positive integer value. For example: 1/1, ½, 1/3, ¼, 1/5, etc.
Decimal
A decimal number can be defined as a number whose fractional part and whole number part are separated by a decimal point. A dot in a decimal number is known as decimal point.
What are the types of Decimals?
Decimal numbers are of two types:
Terminating decimal numbers
Terminating decimal numbers are that types of decimal numbers that have a finite number of digits after the decimal point.
These types of decimal numbers are called exact decimal numbers.
The number of digits after the decimal point in these numbers is countable. For example: 0.2,0.125, 0.35 etc.
Afterdecimal numbers, there are examples of terminating or exact decimal numbersà The sole reason is that the number of digits after the decimal point is finite.
These decimal numbers can be represented in the form of p/q.Therefore, they are known as rational numbers.
Non – terminating decimal numbers
As the name suggests, the numbers that come after the decimal point of non – terminating decimals never end.
In other words, we can say that non-terminating decimal numbers have an infinite number of digits after the decimal point. For example:0.333…,
Non- terminating decimal numbers are further divided into two decimal numbers i.e. Non-recurring decimal numbers and Recurring decimal numbers.
Recurring Decimal Numbers
These types of decimal numbers have an infinite number of digits after the decimal point but these digits are periodic and the infinitely repeated portion is not zero. Recurring decimal is also referred as repeating decimal or terminating decimal. For example: 3.7777, 0.181818 etc.
We can also put a bar sign over the decimal numbers because the numbers follow a specific order. Also, we can write it by placing a dot above the repeating digit 7 in the quotient.
Non-recurring decimal numbers
Non-recurring decimal numbers are the type of decimal numbers that do not only have an infinite number of digits at their decimal places, but their decimal place digits do not follow any type of order. Non-recurring decimal is also referred as non-repeating, non-terminating decimal numbers. For example :π = 3.141592… , e = 2.718….
But we cannot put a bar sign over the decimal numbers because the digits follow no specific order. These type of decimal numbers cannot be written in the form of p/q.Thus, they are also known as irrational numbers.
Note :
Here are some facts which are lesser-known and curious facts about decimals:
- The term ‘Dec’ in decimal means ten and refers to the fact that each position in a decimal number corresponds to ten times more than the next position along. For example, the number 245.89 means 2 hundreds, 4 tens, 5 ones, 8 tenth,s and 9 hundredth.
- Decimal fractions were first used and developed by the Chinese at the end of the 4th century BC and then spread to the Middle East and from there to Europe.
- Some decimal expansions go on forever. For example, 1/3 = 0.333… where the ‘…’ means that the 3s go on forever.
- Every fraction is a decimal. A fraction is one whole number divided by another but we can’t divide by zero. Every fraction positive or negative, small or large can be written as a decimal. For example: ½ = 0.5, 1/3 = 0.333… , 1/5 = 0.25.
- But not every decimal is a fraction. Some numbers are so strange that they can’t be represented in a fractional form. For example, the number π that we use to calculate circle measurements has a decimal expansion that goes on forever and never repeats (it starts at 3.14159). So, it cannot be written in a fractional form.
- For the decimal point, different countries and languages use different notation. For example, in Singapore and Taiwan the point is placed is placed mid-line, so 23·89 rather than 23.89. In many European countries, a comma is used so23,89.
- Decimals are used in various situations in the real world. To represent different amounts i.e. weight, height, and money all use a decimal point. Since, the Richter scale, measures the strength of an earthquake.
What Is 5/8 As A Decimal?
This answer is found by various methods.
Method 1
By the use of the calculator, divide the fraction’s numerator by the denominator.
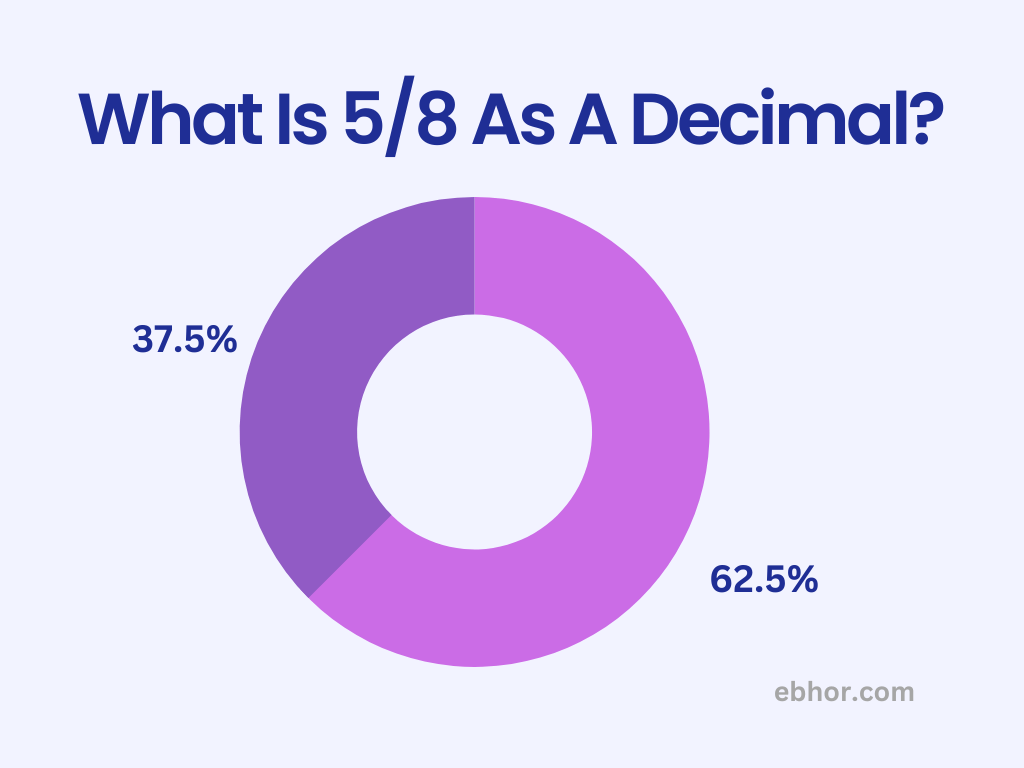
5/8 = 5÷8 = 0.625
Method 2
By the use of long division, divide the fraction’s numerator by the fraction’s denominator.
- Write the numerator five (5) as the dividend and the denominator eight (8) as the divisor.
- Since eight (8)is greater than five (5), place a decimal point in the quotient and add zero (0) to make it fifty (50).
- Eight (8) divides fifty (50) six times to give forty eight (48).
- Subtract forty-eight (48) from fifty (50) to get the remaining of two(2).
- As we have already added the decimal point, we can add zero (0) to two (2) to make it twenty (20).
- Eight (8) divides twenty(20) two times to give sixteen (16).
- Subtract sixteen (16) from twenty (20) to get the remainder four (4).
- Add zero (0) again to make it forty (40).
- Eight (8) divides forty (40) five times to give forty (40).
- Subtract forty (40) from forty (40) to get the remainder zero (0).
Hence, the solution is 0.625.
Method 3
Expand the denominator to be a power of 10,100,1000.
The denominator of the fraction is multiplied by a number that gives the result in terms of 10, 100, 1,000 or another multiple of 10. For the fraction five-eighths (5/8), the denominator of the fraction is 8.
Multiply 8 by 125 to give 1,000. Multiply both the numerator and denominator by 125 and it gives the result 625/1000.
Then write down just the top number, putting the decimal point in the correct spot i.e. one place from the right end for every 0 in the bottom number.
So, decimal point is in the thousandths place. Hence,625/1000 as a decimal equals to 0.625.
Why Would You LikeTo Convert 5/8 InDecimal Form?
There are many calculations on the internet about how can we convert a fraction into decimal form, but the basic question arises that at first place why do you wish, need, or want to convert it in the very 1st place?
Firstly, It is just a good way to show a fraction in a way that allows you to do basic arithmetic with them as addition, subtraction, multiplication, and division.
In real life, we mostly deal with decimals (like currency, for example), and human brains are trained from a very young age to compare and understand decimals more often than they are fractions. So, it is easier if they are converted into a decimal first!
Now, let’s talk about a real-life example that clearly states why the conversion of fractions into their decimal forms is imperative in real life.
Let us assume that you’re cooking and you can usually see fractionally how much of an ingredient is left in a pack. However, electronic scales measure weight in decimalformats rather than fraction of the ingredient left.
This makes converting between decimals and fractions a useful skill in cooking.
We hope that this tutorial has aided you in understanding on how to convert the fraction numbers to their decimal numbers, and why it is important to do so.
You can now go forth and convert fraction numbers to their decimal formats as much as your little heart desires!
Fraction to decimal conversion table
Fraction Decimal
½ = 0.5
1/3 = 0.33333333
2/3 = 0.66666667
¼ = 0.25
2/4 = 0.5
¾ =0.75
1/5 = 0.2
2/5 = 0.4
3/5 = 0.6
4/5 = 0.8
1/6 = 0.16666667
2/6 = 0.33333333
Frequently Asked Questions
- What are the numerator and denominator in a fraction 5/8?
Numerator = 5
Denominator = 8
- Is 5/8 a terminating decimal or a repeating decimal?
A decimal that ends is known as terminating. 5/8 is a terminating decimal expansion because when we divide it we get 0.625.
- What is a ratio equivalent to 5/8?
The two equivalent ratios of 5: 8 are 10: 16 15: 24.
- Is 5/8 a rational or irrational number?
The ratio of an integer a to a non-zero integer b is known as rational number. The general rule is a/b. So, 5/8 is a rational number.
- What is the percent form of 5/8?
For the conversion of a fraction into a percentage, We multiply the given fraction by 100 and add a % symbol to it.
= 5/8 × 100
= 500/8 %
= 62.5 %
Hence, 5/8 is equivalent to 62.5%.
- Why is the decimal for 5/8 of an inch is 0.625, but the decimal for 5/8 of a foot is .0521?
I guess you are confusing 5/8 decimal for an inch is 0.625 inches, is it? But, there are 12 inches in afoot!
Therefore, to convert 5/8 inches to feet, you can simply divide the above decimal answer by 12 like so:
= 0.625 / 12
= 0.05208333 feet