Factors of 65?

The factors of 65 are the numbers that divide 65 evenly, leaving no remainder.

The factors of 65 are 1, 5, 13, and 65.

To find the factors of 65, you can divide 65 by each number between 1 and 65, and any number that divides 65 evenly is a factor.

Here we discuss Factors of 65 Prime Factorization of 65 and other topics.

What Are The Factors?

In Mathematics, factors of 65 are the natural numbers that can divide the number 65 completely.

We can also say that when two natural numbers are multiplied together and they result in 65, then these numbers are known as factors of the number 65.

Stat Check – The number 65 is also an odd composite number.

What Are The Factors Of 65?

65 is a special 2-digit no because apart from one and sixty-five, it has only 1 other pair factor, i.e. 5 and 13.

So, we found that 65 has 4 positive factors and 4 negative factors. These are 1, 5, 13, and 65. Hence, the total number of factors of 65 is 8.

How to Calculate the Factors?

Try 1. One x Sixty-Five = Sixty-Five, so put these into our factor list.

Take 2… no good. 65/2 isn’t a whole number. So we skip 2.

Now take 3… no. 65/3 isn’t a whole number. So we skip 3.

Next, try 4… no luck. 65/4 isn’t a whole number. So we skip 4.

Now try 5…5 x 13 = 65, so put these into our factor list.

Try 6… no good. 65/6 isn’t a whole number. So we skip 6.

Take 7… no. 65/7 isn’t a whole number. So we skip 7.

Now take 8… no luck. 65/8 isn’t a whole number. So we skip 8.

Next try 9… nope! 65/9 isn’t a whole number. So we skip 9.

Now, we don’t have any more numbers to try.

Therefore, factors are 1,5,13,65.

Prime Factorization

The product of prime numbers that will be equal to the original number is known as prime factorization.

Here, we are required to find the prime nos that can completely divide the original no. To find these prime factors, firstly write the prime numbers that occur between 1 and 65.

List of prime numbers (Between 1 and 65) :

• Sixty-One
• Fifty-Nine
• Fifty-Three
• Forty-Seven
• Forty-Three
• Forty-One
• Thirty-Seven
• Thirty-One
• Twenty-Nine
• Twenty-Three
• Nineteen
• Seventeen
• Thirteen
• Eleven
• Seven
• Five
• Three, and
• Two.

From the aforementioned list, we can find the prime factors that can divide 65.

Step 1: We divide it by its smallest prime factor which is 5.

65/5 = 13

Step 2: 13 is a prime number whose factors are 1 and 13.

13/13 = 1

The process of prime factorization goes on till we get the quotient as 1 because 1 is the only factor of itself and is not divisible by any prime number. The number of prime factors of 65 is 2 i.e.

Prime factorization or decomposition of 65 = 5 x 13

It is also written in exponential form i.e.

Exponential Form = 5¹ x 13¹

Factor Pairs Of 65

The factor pairs of 65 are all the different combinations of two factors that when multiplied together equal 65. Hereinafter laid down are all the Positive Factor Pairs of 65.

1 x 65 = 65

5 x 13 = 65

13 x 5 = 65

65 x 1 = 65

As we said above, Factors of 65 also include negative numbers.

Minus multiplies minus equals plus, thus you can convert the Positive Factor Pair list into a negative factor pair list by simply putting a minus sign in front of the above given positive factor pair list.

Here are all the Negative Factor Pairs of 65.

-1 × -65 = 65

-5 × -13 = 65

-13 × -5 = 65

-65 × -1 = 65

Factor Tree Of 65

A special diagram where we find the factors of a number and then the factors of those numbers until we can’t factor them anymore is known as a factor tree.

It is the list of all prime numbers when multiplied given to the original number 65.

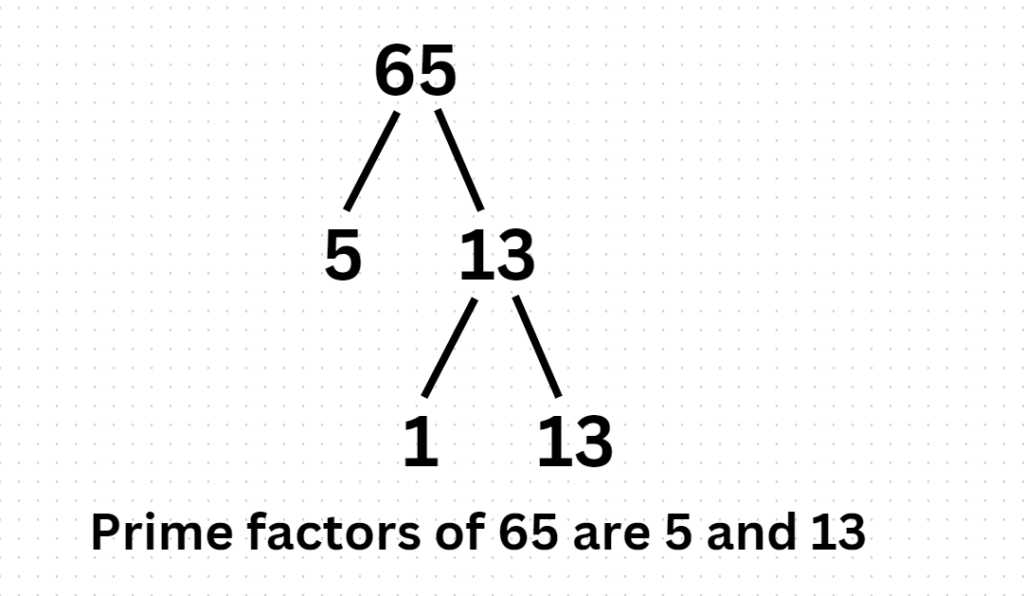
How to find factor tree of 65 ?

• Divide the composite no whose factor tree is to be found by its smallest prime factor.
• If the resulting quotient is a composite no, divide it by its smallest prime factor.
• The process goes on until the resulting quotient is a prime number.

Points To Remember :

• One, Five, Thirteen, and Sixty-Five are the factors of 65.
• The no 65 is neither a perfect square no nor a perfect cube no.
• The numbers which we multiply to obtain sixty-five are the factors of sixty-five.
• As the number 65 is an odd composite number, so all of its factors will also be odd.

Factors Of 65 Questions and Examples