Decimal number is a number where whole number and decimal number are separated by decimal point(.)
Number represented in decimal form in known as Decimal numbers.

Like decimal– the decimal with the same number of decimal places are called like decimal. Example 2.39, 4.57, 23.86.
Unlike decimal– the decimal having different number of decimal places are called unlike decimal.
Conversion of a decimal into a fraction
- Write the given number without decimal point as the numerator of the fraction- 6:25 —-> 625
- In the denominator write 1 followed by as many zero as there are decimal places in the given number 625/100
- Convert the above fraction into simplest form.
Conversion of a fraction into a decimal.
- When the denominator of a fraction is 10 or its multiple. for example
=
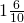 =1.6 or
=1.6 or =1.6
- Equivalent fraction method
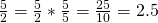

3. Division method![]()
Decimal fraction–
1) Decimal fraction–
fractions in which denominator are powers of 10 are known a decimal fraction.
Thus ![]() = 1 tenth = 0.1,
= 1 tenth = 0.1,![]() = 1 hundredth = 0.01,
= 1 hundredth = 0.01,![]() = 99 hundredth = 0.99
= 99 hundredth = 0.99![]() = 7 thousandths = .007 etc.
= 7 thousandths = .007 etc.
2) Conversion of a decimal into vulgar fraction:-
put 1 in the denominator under the decimal point & annexure with it as many zero as is the number of digits after the decimal points now remove the decimal point & reduce the fraction of its lowest term.![]()
![]()
3) i) annexing zero to the extreme right of a decimal fraction does not change its value. Thus 0.80= 0.800 etc.
ii) if numerator & denominator of a fraction contain the same number of decimal places then we move the decimal sign.
Thus, ![]()
![]()
Operation on decimal fraction
) Addition & Substraction– given number are so placed under each other that the decimal points lie in the correspondent column and now be added or subtracted in the usual way.
ii) Multiplication of a decimal fraction by a power of 10 Shift the decimal point to the right by as many phase as is the power of 10
4.31 10 43.1/10
4.6987 1000 = 4698.7/1000
iii) Multiplication of decimal fraction:-
multiply the given numbers considering them without the decimal point.
Now in the product, the decimal point is marked of to obtain an any places of decimal as is the sum of the number of decimal places in the given number.
Example ![]()
(sum of decimal places 1+1+1+3=6 no.)
iv) Dividing a decimal fraction by a converting number–
divide the given number without considering the decimal point by the given counting number now in the quotient put the decimal point to give as many places of decimal as there are in the dividend.
Example![]()
v) Dividing a decimal fraction by a decimal fraction
thus, ![]() or
or ![]()
Comparison of fraction–
fractions are to be arranged in ascending or dis cending order of magnitude, then convert each one of the given fraction in the decimal form & arrange them accordingly.![]()
![]()
Here ![]()
So ![]() >
>![]()
![]()
LCM of ![]()
![]()
Here ![]()
So ![]()
vi) Recurring decimal–
if in a decimal fraction, a figure or a set of figures is repeated continuously then such a number is called a recurring decimal thus.![]() ,
,![]()
Pure recurring decimal–
A decimal fraction in which all the figure. After the decimal point are repeated is called a pure recurring decimal.
Converting a pure recurring decimal into vulgar fraction
![]()
![]()
![]()
Write the repeated figures only one in numerator & take as many mix in the denominators as is the number of repeating figure.
Mixed recurring decimal–
A decimal fraction in which some figure do not repeat & some of them are repeated, is called mixed recurring decimal.
Example ![]()
Converting a mixed recurring decimal into vulgar fraction
In the numerator take the difference between the number formed by all the digit after decimal point . (taking repeated digit only once) & that formed by digit which are not repeated.
In the denominator take the number formed by as many as there are repeating digit followed by as many zeros as is the number of non repeating digits.
Thus,![]()
![]()
Read More
